7 αλγόριθμοι που πρέπει να γνωρίζει κάθε προγραμματιστής

Ως φοιτητής προγραμματισμού, πιθανότατα έχετε μάθει πολλούς διαφορετικούς αλγόριθμους κατά τη διάρκεια της καριέρας σας. Το να είσαι ικανός σε διαφορετικούς αλγόριθμους είναι απολύτως απαραίτητο για κάθε προγραμματιστή.

Με τόσους αλγόριθμους, μπορεί να είναι δύσκολο να παρακολουθείτε τι είναι απαραίτητο. Εάν προετοιμάζεστε για μια συνέντευξη ή απλώς βελτιώνετε τις ικανότητές σας, αυτή η λίστα θα το κάνει σχετικά εύκολο. Διαβάστε παρακάτω καθώς παραθέτουμε τους πιο βασικούς αλγόριθμους για προγραμματιστές.

1. Ο αλγόριθμος του Dijkstra

Ο Edsger Dijkstra ήταν ένας από τους πιο σημαντικούς επιστήμονες υπολογιστών της εποχής του και συνέβαλε σε αυτό πολλούς διαφορετικούς τομείς της επιστήμης των υπολογιστών, συμπεριλαμβανομένων των λειτουργικών συστημάτων, της κατασκευής μεταγλωττιστή και πολλά άλλα περισσότερο. Μία από τις πιο αξιοσημείωτες συνεισφορές του Dijkstra είναι η εφευρετικότητα του αλγορίθμου συντομότερης πορείας του για γραφήματα, γνωστού και ως αλγόριθμος συντομότερης πορείας του Dijkstra.

Ο αλγόριθμος του Dijkstra βρίσκει την πιο σύντομη διαδρομή σε ένα γράφημα από μια πηγή προς όλες τις κορυφές γραφήματος. Σε κάθε επανάληψη του αλγορίθμου, προστίθεται μια κορυφή με την ελάχιστη απόσταση από την πηγή και μία που δεν υπάρχει στην τρέχουσα συντομότερη διαδρομή. Αυτή είναι η άπληστη ιδιότητα που χρησιμοποιείται από τον αλγόριθμο του Djikstra.

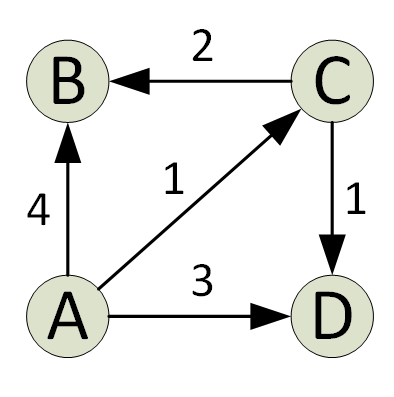
Ο αλγόριθμος εφαρμόζεται συνήθως χρησιμοποιώντας ένα σύνολο. Ο αλγόριθμος του Dijkstra είναι πολύ αποτελεσματικός όταν εφαρμόζεται με ένα Min Heap. μπορείτε να βρείτε τη συντομότερη διαδρομή σε χρόνο O (V+ElogV) (V είναι ο αριθμός των κορυφών και E είναι ο αριθμός των ακμών σε ένα δεδομένο γράφημα).

Ο αλγόριθμος του Dijkstra έχει τους περιορισμούς του. λειτουργεί μόνο σε κατευθυνόμενα και μη κατευθυνόμενα γραφήματα με ακμές θετικού βάρους. Για αρνητικά βάρη, ο αλγόριθμος Bellman-Ford είναι συνήθως προτιμότερος.

Οι ερωτήσεις συνέντευξης περιλαμβάνουν συνήθως τον αλγόριθμο του Djikstra, επομένως συνιστούμε να κατανοήσετε τις περίπλοκες λεπτομέρειες και εφαρμογές του.

2. Συγχώνευση Ταξινόμηση

Έχουμε δύο αλγόριθμους ταξινόμησης σε αυτήν τη λίστα και η ταξινόμηση συγχώνευσης είναι ένας από τους πιο σημαντικούς αλγορίθμους. Είναι ένας αποτελεσματικός αλγόριθμος ταξινόμησης που βασίζεται στην τεχνική προγραμματισμού Divide and Conquer. Σε ένα χειρότερο σενάριο, η ταξινόμηση συγχώνευσης μπορεί να ταξινομήσει αριθμούς "n" σε χρόνο O (nlogn). Σε σύγκριση με τις πρωτόγονες τεχνικές διαλογής όπως π.χ. Ταξινόμηση φυσαλίδων (που απαιτεί χρόνο O (n^2)), η ταξινόμηση συγχώνευσης είναι εξαιρετικά αποτελεσματική.

Σχετίζεται με: Εισαγωγή στον αλγόριθμο συγχώνευσης ταξινόμησης

Στην ταξινόμηση συγχώνευσης, ο πίνακας που θα ταξινομηθεί αναλύεται επανειλημμένα σε υποσυστοιχίες έως ότου κάθε υποσυστοιχία αποτελείται από έναν μόνο αριθμό. Ο επαναληπτικός αλγόριθμος στη συνέχεια συγχωνεύει επανειλημμένα τις υποσυστοιχίες και ταξινομεί τον πίνακα.

3. Γρήγορη ταξινόμηση

Το Quicksort είναι ένας άλλος αλγόριθμος ταξινόμησης που βασίζεται στην τεχνική προγραμματισμού Divide and Conquer. Σε αυτόν τον αλγόριθμο, ένα στοιχείο επιλέγεται αρχικά ως περιστροφικός άξονας και στη συνέχεια ολόκληρος ο πίνακας χωρίζεται γύρω από αυτόν τον άξονα περιστροφής.

Όπως πιθανώς μαντέψατε, ένας καλός άξονας είναι ζωτικής σημασίας για μια αποτελεσματική ταξινόμηση. Ο άξονας περιστροφής μπορεί είτε να είναι ένα τυχαίο στοιχείο, το στοιχείο πολυμέσων, το πρώτο στοιχείο ή ακόμα και το τελευταίο στοιχείο.

Οι εφαρμογές του quicksort συχνά διαφέρουν στον τρόπο που επιλέγουν έναν άξονα. Στη μέση περίπτωση, το quicksort θα ταξινομήσει έναν μεγάλο πίνακα με έναν καλό άξονα σε χρόνο O (nlogn).

Ο γενικός ψευδοκώδικας του quicksort χωρίζει επανειλημμένα τον πίνακα στον άξονα και τον τοποθετεί στη σωστή θέση του υποσυστοιχίου. Τοποθετεί επίσης τα στοιχεία μικρότερα από τον άξονα στα αριστερά του και στοιχεία μεγαλύτερα από τον άξονα στα δεξιά του.

4. Πρώτη αναζήτηση βάθους

Το Depth First Search (DFS) είναι ένας από τους πρώτους αλγόριθμους γραφημάτων που διδάχθηκαν στους μαθητές. Το DFS είναι ένας αποτελεσματικός αλγόριθμος που χρησιμοποιείται για να διασχίσει ή να αναζητήσει ένα γράφημα. Μπορεί επίσης να τροποποιηθεί για χρήση σε δέντρα διασχίσεων.

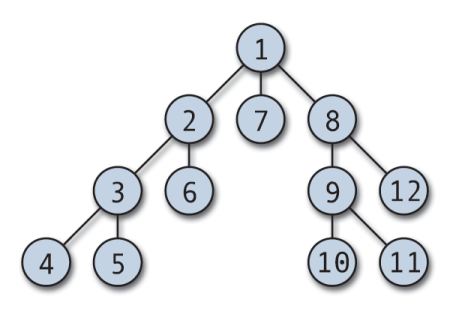
Η διέλευση DFS μπορεί να ξεκινήσει από οποιονδήποτε αυθαίρετο κόμβο και βουτά σε κάθε γειτονική κορυφή. Ο αλγόριθμος υποχωρεί όταν δεν υπάρχει κορυφή χωρίς επίσκεψη ή υπάρχει αδιέξοδο. Το DFS εφαρμόζεται συνήθως με μια στοίβα και έναν πίνακα boolean για να παρακολουθεί τους κόμβους που επισκέπτεται. Το DFS είναι απλό στην εφαρμογή και εξαιρετικά αποτελεσματικό. λειτουργεί (V+E), όπου V είναι ο αριθμός των κορυφών και E είναι ο αριθμός των ακμών.

Οι τυπικές εφαρμογές της διέλευσης DFS περιλαμβάνουν τοπολογική ταξινόμηση, ανίχνευση κύκλων σε γράφημα, ανίχνευση διαδρομής και εύρεση ισχυρά συνδεδεμένων στοιχείων.

5. Πλάτος-Πρώτη αναζήτηση

Breadth-First Search (BFS) είναι επίσης γνωστή ως διασταύρωση επιπέδου για δέντρα. Το BFS λειτουργεί σε O (V+E) παρόμοιο με έναν αλγόριθμο DFS. Ωστόσο, το BFS χρησιμοποιεί μια ουρά αντί για τη στοίβα. Το DFS βυθίζεται στο γράφημα, ενώ το BFS διασχίζει το γράφημα κατά πλάτος.

Ο αλγόριθμος BFS χρησιμοποιεί μια ουρά για να παρακολουθεί τις κορυφές. Οι γειτονικές κορυφές χωρίς επίσκεψη επισκέπτονται, επισημαίνονται και τίθενται σε ουρά. Εάν η κορυφή δεν έχει παρακείμενη κορυφή, τότε μια κορυφή αφαιρείται από την ουρά και διερευνάται.

Το BFS χρησιμοποιείται συνήθως σε δίκτυα peer-to-peer, τη συντομότερη διαδρομή ενός μη σταθμισμένου γραφήματος και την εύρεση του ελάχιστου δέντρου που εκτείνεται.

6. Δυαδική αναζήτηση

Δυαδική αναζήτηση είναι ένας απλός αλγόριθμος για να βρείτε το απαιτούμενο στοιχείο σε έναν ταξινομημένο πίνακα. Λειτουργεί διαιρώντας επανειλημμένα τον πίνακα στο μισό. Εάν το απαιτούμενο στοιχείο είναι μικρότερο από το μεσαίο στοιχείο, τότε η αριστερή πλευρά του μεσαίου στοιχείου υποβάλλεται σε περαιτέρω επεξεργασία. Διαφορετικά, η δεξιά πλευρά μειώνεται στο μισό και αναζητείται ξανά. Η διαδικασία επαναλαμβάνεται μέχρι να βρεθεί το απαιτούμενο στοιχείο.

Η πιο περίπλοκη χρονική πολυπλοκότητα της δυαδικής αναζήτησης είναι το O (logn) που το καθιστά πολύ αποτελεσματικό στην αναζήτηση γραμμικών πινάκων.

7. Ελάχιστοι αλγόριθμοι έκτασης δέντρων

Ένα ελάχιστο δέντρο έκτασης (MST) ενός γραφήματος έχει το ελάχιστο κόστος μεταξύ όλων των πιθανών εκτεινόμενων δέντρων. Το κόστος ενός δέντρου που εκτείνεται εξαρτάται από το βάρος των άκρων του. Είναι σημαντικό να σημειωθεί ότι μπορεί να υπάρχουν περισσότερα από ένα ελάχιστα δέντρα έκτασης. Υπάρχουν δύο κύριοι αλγόριθμοι MST, συγκεκριμένα οι Kruskal's και Prim's.

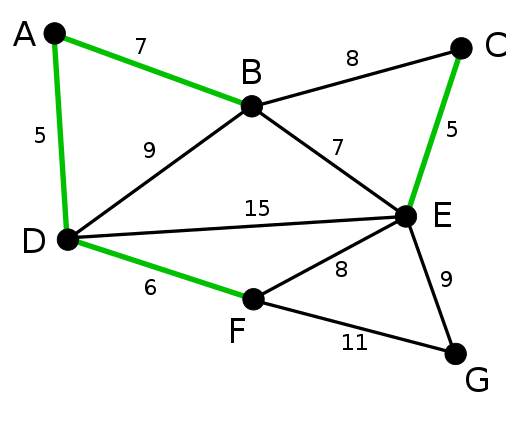
Ο αλγόριθμος του Kruskal δημιουργεί το MST προσθέτοντας την άκρη με ελάχιστο κόστος σε ένα αναπτυσσόμενο σύνολο. Ο αλγόριθμος ταξινομεί πρώτα τις άκρες κατά το βάρος τους και στη συνέχεια προσθέτει άκρες στο MST ξεκινώντας από το ελάχιστο.

Είναι σημαντικό να σημειωθεί ότι ο αλγόριθμος δεν προσθέτει ακμές που σχηματίζουν έναν κύκλο. Ο αλγόριθμος του Kruskal προτιμάται για αραιά γραφήματα.

Ο αλγόριθμος Prim χρησιμοποιεί επίσης μια άπληστη ιδιότητα και είναι ιδανικός για πυκνά γραφήματα. Η κεντρική ιδέα στο MST του Prim είναι να έχουμε δύο ξεχωριστά σύνολα κορυφών. το ένα σύνολο περιέχει το αυξανόμενο MST, ενώ το άλλο περιέχει αχρησιμοποίητες κορυφές. Σε κάθε επανάληψη, επιλέγεται το ελάχιστο άκρο βάρους που θα συνδέει τα δύο σύνολα.

Οι ελάχιστοι αλγόριθμοι εκτάσεων δέντρων είναι απαραίτητοι για την ανάλυση συμπλεγμάτων, την ταξινόμηση και τα δίκτυα εκπομπής.

Ένας αποτελεσματικός προγραμματιστής είναι ικανός με αλγόριθμους

Οι προγραμματιστές μαθαίνουν και αναπτύσσουν συνεχώς τις δεξιότητές τους και υπάρχουν ορισμένα βασικά βασικά στοιχεία για τα οποία όλοι πρέπει να είναι ικανοί. Ένας εξειδικευμένος προγραμματιστής γνωρίζει τους διαφορετικούς αλγόριθμους, τα οφέλη και τα μειονεκτήματα του καθενός και ποιος αλγόριθμος θα ήταν ο καταλληλότερος για ένα δεδομένο σενάριο.

Εισαγωγή στον αλγόριθμο ταξινόμησης Shell

Ενώ η ταξινόμηση κελύφους δεν είναι η πιο αποτελεσματική μέθοδος, οι αρχάριοι έχουν πολλά να κερδίσουν από την εξάσκηση.

Διαβάστε Επόμενο

Σχετικά με τον Συγγραφέα