Τι είναι το δυαδικό; [Η τεχνολογία εξηγείται]

Διαφήμιση

Δεδομένου ότι το δυαδικό είναι τόσο απολύτως θεμελιώδες για την ύπαρξη υπολογιστών, φαίνεται περίεργο που δεν έχουμε αντιμετωπίσει ποτέ θέμα πριν - οπότε σήμερα σκέφτηκα ότι θα έδινα μια σύντομη επισκόπηση του τι σημαίνει πραγματικά το δυαδικό και πώς χρησιμοποιείται Υπολογιστές. Αν αναρωτιόσασταν πάντα ποια είναι η διαφορά 8-bit, 32-bit, και 64-bit είναι πραγματικά και γιατί έχει σημασία - τότε διαβάστε!

Τι είναι το δυαδικό; Η διαφορά μεταξύ της βάσης 10 και της βάσης 2

Οι περισσότεροι από εμάς έχουν μεγαλώσει σε έναν κόσμο 10 βασικών αριθμών, με τον οποίο εννοώ ότι έχουμε 10 'βάση' αριθμοί (0-9) από την οποία αντλούμε όλους τους άλλους αριθμούς. Μόλις τα εξαντλήσουμε, ανεβαίνουμε ένα επίπεδο μονάδας - 10, 100, 1000 - αυτή η μορφή μέτρησης σφυρηλατείται στον εγκέφαλό μας από τη γέννηση. Στην πραγματικότητα, μόνο από τη Ρωμαϊκή περίοδο ξεκινήσαμε να μετράμε στη βάση 10. Πριν από αυτό, η βάση 12 ήταν η ευκολότερη και οι άνθρωποι χρησιμοποιούσαν τις αρθρώσεις τους για να μετρήσουν.

Όταν μαθαίνουμε τη βάση 10 στο δημοτικό σχολείο, γράφουμε συχνά τις ενότητες ως εξής:

Ο αριθμός λοιπόν 1990 πραγματικά αποτελείται από 1 x 1000, 9 x 100, 9 x 10, και 0 x 1. Δεν είμαι σίγουρος ότι δεν χρειάζεται να εξηγήσω τη βάση 10 περισσότερο από αυτό.

Αλλά τι γίνεται αν αντί να έχετε μια πλήρη επιλογή 0,1,2,3,4,5,6,7,8,9 να δουλέψουμε με τους βασικούς αριθμούς - τι γίνεται αν είχαμε μόνο 0, και 1. Αυτό ονομάζεται βάση 2; και αναφέρεται επίσης ως δυάδικος. Σε έναν δυαδικό κόσμο, μπορείτε να μετρήσετε μόνο 0,1 - τότε πρέπει να μεταβείτε στο επόμενο επίπεδο μονάδας.

Μετρώντας στο δυαδικό

Βοηθά πάρα πολύ αν γράψουμε τις ενότητες όταν μαθαίνουμε δυαδικά. Σε αυτήν την περίπτωση, αντί κάθε πολλαπλασιαστικής μονάδας να πολλαπλασιάζεται με 10, πολλαπλασιάζεται με 2, δίνοντάς μας 1,2,4,8,16,32,64 … Έτσι, για να υπολογίσουμε, μπορούμε να τα γράψουμε ως εξής:

Με άλλα λόγια, η σωστή τιμή σε δυαδικό αριθμό αντιπροσωπεύει τον αριθμό 1. Το επόμενο ψηφίο, στα αριστερά του, αντιπροσωπεύει τον αριθμό των 2. Το επόμενο αντιπροσωπεύει πόσα 4… και έτσι.

Με αυτήν τη γνώση, μπορούμε να γράψουμε έναν πίνακα μέτρησης σε δυαδικό, με την ισοδύναμη τιμή βάσης 10 να φαίνεται στα αριστερά.

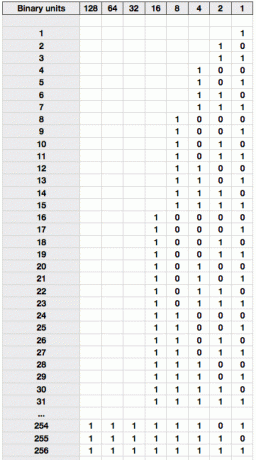
Περάστε μια στιγμή για να το δείτε μέχρι να δείτε ακριβώς γιατί το 25 γράφεται ως 11001. Θα πρέπει να μπορείτε να το αναλύσετε ως 16 + 8 + 1 = 25.

Εργασία προς τα πίσω - βάση 10 έως δυαδικό

Τώρα θα πρέπει να μπορείτε να καταλάβετε τι αξία έχει ένας δυαδικός αριθμός σχεδιάζοντας έναν παρόμοιο πίνακα και πολλαπλασιάζοντας κάθε μονάδα. Η εναλλαγή ενός κανονικού αριθμού βάσης 10 σε δυαδικό απαιτεί λίγο περισσότερη προσπάθεια. Το πρώτο βήμα είναι να βρείτε τη μεγαλύτερη δυαδική μονάδα που «ταιριάζει» στον αριθμό. Για παράδειγμα, αν κάναμε 35, τότε ο μεγαλύτερος αριθμός από αυτόν τον πίνακα που χωράει στο 35 είναι 32, οπότε θα έχουμε 1 εκεί στη στήλη. Έχουμε λοιπόν ένα υπόλοιπο 3 - το οποίο θα χρειαζόταν ένα 2 και τελικά ένα 1. Λοιπόν 100011.

8-bits, Bytes και Octets

Ο πίνακας που έχω δείξει παραπάνω είναι 8-bit, επειδή έχουμε το πολύ 8 μηδενικά και αυτά που θα χρησιμοποιήσουμε για τον δυαδικό μας αριθμό. Έτσι, ο μέγιστος αριθμός που πιθανώς μπορούμε να αντιπροσωπεύσουμε είναι 11111111, ή 255. Αυτός είναι ο λόγος για να αντιπροσωπεύσετε οποιονδήποτε αριθμό από 0-255, χρειαζόμαστε τουλάχιστον 8-bit. Το Octet και το Byte είναι απλά ένας άλλος τρόπος για να πούμε 8-bit. Ως εκ τούτου 1 Byte = 8 bit.

Υπολογισμός 32 έναντι 64-bit

Σήμερα ακούτε συχνά τους όρους 32-bit και 64-bit εκδόσεις των Windows και ίσως γνωρίζετε ότι τα Windows 32-bit μπορούν να υποστηρίξουν μόνο έως 4 gigabyte RAM. Γιατί συμβαίνει αυτό;

Όλα έρχονται στη διεύθυνση μνήμης. Κάθε bit μνήμης χρειάζεται μια μοναδική διεύθυνση για να έχει πρόσβαση. Αν είχαμε ένα 8-bit σύστημα διευθύνσεων μνήμης, θα μπορούσαμε να έχουμε μόνο ένα μέγιστο 256 byte μνήμης. Με 32-bit σύστημα διευθύνσεων μνήμης (Φανταστείτε να επεκτείνετε τον παραπάνω πίνακα για να έχετε 32 στήλες δυαδικής μονάδας), μπορούμε να πάμε οπουδήποτε μέχρι 4,294,967,296? 4 δισεκατομμύρια byteή με άλλα λόγια - 4 GIGAbyte.64-bit Ο υπολογιστής καταργεί ουσιαστικά αυτό το όριο, δίνοντάς μας έως 18 δισεκατομμύρια διαφορετικές διευθύνσεις - ένας αριθμός από τους περισσότερους απλώς δεν μπορούμε να κατανοήσουμε.

Διεύθυνση IPv4

Η τελευταία ανησυχία στον κόσμο των υπολογιστών είναι το παν σχετικά με τις διευθύνσεις IP IPv6 & The Coming ARPAgeddon [Επεξήγηση τεχνολογίας] Διαβάστε περισσότερα , συγκεκριμένα IPv4 διευθύνσεις, όπως αυτές:

• 192.168.0.1
• 200.187.54.22

Στην πραγματικότητα αποτελούνται από 4 αριθμούς, ο καθένας αντιπροσωπεύει μια τιμή έως 255. Μπορείτε να μαντέψετε γιατί; Ναι, ολόκληρη η διεύθυνση αντιπροσωπεύεται από 4 οκτάδες (32 bit συνολικά). Φαινόταν σαν μια τεράστια πιθανή διεύθυνση (περίπου 4 δισεκατομμύρια στην πραγματικότητα) τη στιγμή που το Διαδίκτυο εφευρέθηκε για πρώτη φορά, αλλά εξαντλούμε γρήγορα τώρα ότι όλα στη ζωή μας πρέπει να συνδεθούν. Για να επιλυθεί αυτό, χρησιμοποιεί το νέο IPv6 128 bit συνολικά, δίνοντάς μας περίπου 340 undecillion (βάλτε 38 μηδενικά στο τέλος) διευθύνσεις για να παίξετε.

Θα το αφήσω εκεί για σήμερα, ώστε να μπορέσω να επιστρέψω στον αρχικό μου στόχο που ήταν να γράψω το επόμενο σεμινάριο Arduino - στο οποίο κάνουμε εκτεταμένη χρήση ενός μητρώου bit-shift. Ελπίζω σήμερα να σας δώσει μια βασική κατανόηση του πόσο δυαδικό είναι τόσο σημαντικό για τους υπολογιστές, γιατί οι ίδιοι αριθμοί συνεχίζουν να εμφανίζονται και γιατί ο αριθμός των bits πρέπει να αντιπροσωπεύσουμε κάτι που θέτει ένα περιορισμένο όριο στην ποσότητα μνήμης, το μέγεθος της οθόνης, τις πιθανές τιμές χρώματος ή τις μοναδικές διευθύνσεις IP που είναι διαθέσιμες σε εμάς. Την επόμενη φορά, θα ρίξουμε μια ματιά υπολογισμοί δυαδικής λογικής, κάτι που κάνει σχεδόν όλοι οι επεξεργαστές υπολογιστών, καθώς και πώς οι υπολογιστές μπορούν να αντιπροσωπεύουν αρνητικούς αριθμούς.

Σχόλια? Σύγχυση? Βρήκατε την εξήγησή μου κατανοητή; Σε κάθε περίπτωση, επικοινωνήστε με τα σχόλια. Θα σε αφήσω με ένα δυαδικό αστείο!

Υπάρχουν μόνο 10 τύποι ανθρώπων στον κόσμο: αυτοί που καταλαβαίνουν δυάδικος, και εκείνοι που δεν το κάνουν.

Πιστωτική εικόνα: Σάττερκοκ